The tradeoff between space and time exploited in dynamic programming is best illustrated in evaluating recurrence relations, such as the Fibonacci numbers. The Fibonacci numbers were originally defined by the Italian mathematician Fibonacci in the thirteenth century to model the growth of rabbit populations. Rabbits breed, well, like rabbits. Fibonacci surmised that the number of pairs of rabbits born in a given year is equal to the number of pairs of rabbits born in each of the two previous years, if you start with one pair of rabbits in the first year. To count the number of rabbits born in the nth year, he defined the following recurrence relation:
with basis cases
and
.
Thus
,
, and the series continues
.
As it turns out, Fibonacci's formula didn't do a very
good job of counting rabbits,
but it does have a host of other applications and interesting properties.
Since they are defined by a recursive formula, it is easy to write a recursive program to compute the nth Fibonacci number. Most students have to do this in one of their first programming courses. Indeed, I have particularly fond memories of pulling my hair out writing such a program in 8080 assembly language. In pseudocode, the recursive algorithm looks like this:
Fibonacci[n]
if (n=0) then return(0)
else if (n=1) then return(1)
else return(Fibonacci[n-1]+Fibonacci[n-2])
Figure: The computation tree for computing Fibonacci numbers recursively
How much time does this algorithm take to compute Fibonacci[n]?
Since
,
this means that
.
Since our recursion tree, illustrated in Figure
,
has only 0 and 1 as
leaves, summing up to such a large number
means we must have at least
leaves or procedure calls!
This humble little program takes exponential time to run!
In fact, we can do much better.
We can calculate in linear time by storing all values.
We trade space for time in the algorithm below:
Fibonacci[n]
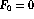
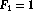
For i=1 to n,
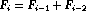
Because we evaluate the Fibonacci numbers from smallest to biggest
and store all the results, we know that we have and
ready whenever we need to compute
.
Thus each of the n values is computed as the simple sum of two integers
in total O(n) time, which is quite an improvement over exponential time.