Figure: Two different triangulations of a given convex seven-gon
A triangulation of a polygon 
is a set of non-intersecting diagonals
that partitions the polygon into triangles.
We say that the weight of a triangulation is the sum
of the lengths of its diagonals.
As shown in Figure 
, any given polygon may
have many different triangulations.
For any given polygon, we seek to find its minimum weight triangulation.
Triangulation is a fundamental component of most geometric algorithms,
as discussed in Section .
To apply dynamic programming, we need a way to carve up the
polygon into smaller pieces.
A first idea might be to try all 
possible chords,
each of which partitions the polygon into two smaller polygons.
Using dynamic programming, this will work to give a polynomial-time
algorithm.
However, there is a slicker approach.
Figure: Selecting the vertex k to pair with an edge (i,j) of the polygon
Observe that every edge of the input polygon must be involved in
exactly one triangle.
Turning this edge into a triangle means identifying
the third vertex, as shown in Figure .
Once we find the correct connecting vertex, the polygon will be partitioned
into two smaller pieces, both of which need to be triangulated optimally.
Let T[i,j] be the cost of triangulating from vertex 
to vertex 
,
ignoring the length of the chord 
from to .
The latter clause avoids double counting these internal chords in the
following recurrence:
The basis condition applies when i and j are immediate neighbors, as T[i,i+1] = 0.
Since the number of vertices in each subrange of the right side of the recurrence is smaller than that on the left side, evaluation can proceed in terms of the gap size from i to j:
Minimum-Weight-Triangulation(P)
for i=1 to n do T[i, j]=0
for gap=1 to n-1
for i=1 to n-gap do
j=i+gap
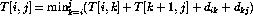
return T[1, n]
There are values of T,
each of which takes O(j-i) time if we evaluate the sections in order
of increasing size.
Since j-i = O(n), complete evaluation takes 
time and 
space.
What if there are points in the interior of the polygon?
Then dynamic programming does not apply in the same way, because each
of the triangulation edges
does not necessarily cut the boundary into two distinct pieces as before.
Instead of only possible subregions, the number
of subregions now grows exponentially.
In fact, no efficient algorithm for this problem is known.
More surprisingly, there is also no known proof of hardness.
Minimum weight triangulation is one of the few well-studied algorithmic
problems that remain in this limbo state.