Lecture Schedule
| subject | topics | reading |
| Preliminaries | Analyzing algorithms | 1-32 |
| " | Asymptotic notation | 32-37 |
| " | Recurrence relations | 53-64 |
| Sorting | Heapsort | 140-150 |
| " | Quicksort | 153-167 |
| " | Linear Sorting | 172-182 |
| Searching | Data structures | 200-215 |
| " | Binary search trees | 244-245 |
| " | Red-Black trees:insertion | 262-272 |
| `` | Red-Black trees:deletion | 272-277 |
| MIDTERM 1 | ||
| Comb. Search | Backtracking | |
| " | Elements of dynamic programming | 301-314 |
| " | Examples of dynamic programming | 314-323 |
| Graph Algorithms | Data structures | 465-477 |
| for graphs | ||
| " | Breadth/depth-first search | 477-483 |
| " | Topological Sort/Connectivity | 485-493 |
| " | Minimum Spanning Trees | 498-510 |
| " | Single-source shortest paths | 514-532 |
| " | All-pairs shortest paths | 550-563 |
| MIDTERM 2 | ||
| Intractability | P and NP | 916-928 |
| " | NP-completeness | 929-939 |
| " | NP-completeness proofs | 939-951 |
| " | Further reductions | 951-960 |
| " | Approximation algorithms | 964-974 |
| " | Set cover / knapsack heuristics | 974-983 |
| FINAL EXAM |
What Is An Algorithm?
Algorithms are the ideas behind computer programs.
An algorithm is the thing which stays the same whether the program is in Pascal running on a Cray in New York or is in BASIC running on a Macintosh in Kathmandu!
To be interesting, an algorithm has to solve a general, specified problem. An algorithmic problem is specified by describing the set of instances it must work on and what desired properties the output must have.
Example: Sorting
Output: the permutation (reordering) of the input sequence such as
.
We seek algorithms which are correct and efficient.
Correctness
For sorting, this means even if (1) the input is already sorted, or (2) it contains repeated elements.
Correctness is Not Obvious!
The following problem arises often in manufacturing and transportation testing applications.
Suppose you have a robot arm equipped with a tool, say a soldering iron. To enable the robot arm to do a soldering job, we must construct an ordering of the contact points, so the robot visits (and solders) the first contact point, then visits the second point, third, and so forth until the job is done.
Since robots are expensive, we need to find the order which minimizes the time (ie. travel distance) it takes to assemble the circuit board.
Nearest Neighbor Tour
A very popular solution starts at some point
and then walks to its nearest neighbor
first,
then repeats from
, etc. until done.
Pick and visit an initial point
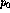
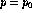
i = 0
While there are still unvisited points
i = i+1
Let
be the closest unvisited point to
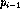
Visit
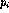
Return to
from
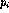
This algorithm is simple to understand and implement and very efficient. However, it is not correct!
Closest Pair Tour
Always walking to the closest point is too restrictive, since that point might trap us into making moves we don't want.
Another idea would be to repeatedly connect the closest pair of points whose connection will not cause a cycle or a three-way branch to be formed, until we have a single chain with all the points in it.
Let n be the number of points in the set
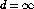
For i=1 to n-1 do
For each pair of endpoints (x,y) of partial paths
If
then
,
, d = dist(x,y)
Connect
by an edge
Connect the two endpoints by an edge.
Although it works correctly on the previous example, other data causes trouble:
A Correct Algorithm
We could try all possible orderings of the points, then select the ordering which minimizes the total length:
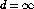
For each of the n! permutations
of the n points
If
then
and
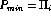
Return
Since all possible orderings are considered, we are guaranteed to end up with the shortest possible tour.
Because it trys all n! permutations, it is extremely slow, much too slow to use when there are more than 10-20 points.
No efficient, correct algorithm exists for the traveling salesman problem, as we will see later.
Efficiency
"Why not just use a supercomputer?"
Supercomputers are for people too rich and too stupid to design efficient algorithms!
A faster algorithm running on a slower computer will always win for sufficiently large instances, as we shall see.
Usually, problems don't have to get that large before the faster algorithm wins.
Expressing Algorithms
In order of increasing precision, we have English, pseudocode, and real programming languages. Unfortunately, ease of expression moves in the reverse order.
I prefer to describe the ideas of an algorithm in English, moving to pseudocode to clarify sufficiently tricky details of the algorithm.
The RAM Model
Algorithms are the only important, durable, and original part of computer science because they can be studied in a machine and language independent way.
The reason is that we will do all our design and analysis for the RAM model of computation:
We measure the run time of an algorithm by counting the number of steps.
This model is useful and accurate in the same sense as the flat-earth model (which is useful)!
Best, Worst, and Average-Case
The worst case complexity of the algorithm is the function defined by the maximum number of steps taken on any instance of size n.
The average-case complexity of the algorithm is the function defined by an average number of steps taken on any instance of size n.
Each of these complexities defines a numerical function - time vs. size!
Insertion Sort
One way to sort an array of n elements is to start with empty list,
then successively insert new elements in the proper position:
At each stage, the inserted element leaves a sorted list, and after n insertions contains exactly the right elements. Thus the algorithm must be correct.
But how efficient is it?
Note that the run time changes with the permutation instance! (even for a fixed size problem)
How does insertion sort do on sorted permutations?
How about unsorted permutations?
Exact Analysis of Insertion Sort
Count the number of times each line of pseudocode will be executed.
| Line | InsertionSort(A) | #Inst. | #Exec. |
| 1 | for j:=2 to len. of A do | c1 | n |
| 2 | key:=A[j] | c2 | n-1 |
| 3 | /* put A[j] into A[1..j-1] */ | c3=0 | / |
| 4 | i:=j-1 | c4 | n-1 |
| 5 | while | c5 | tj |
| 6 | A[i+1]:= A[i] | c6 | |
| 7 | i := i-1 | c7 | |
| 8 | A[i+1]:=key | c8 | n-1 |
Within the for statement, "key:=A[j]" is executed n-1 times.
Steps 5, 6, 7 are harder to count.
Let the number of elements that have to be slide right
to insert the jth item.
Step 5 is executed times.
Step 6 is .
Add up the executed instructions for all pseudocode lines to get the run-time of the algorithm:
What are the ?
They depend on the particular input.
Best Case
Hence, the best case time is
where C and D are constants.
Worst Case