Input description: An matrix A and a
matrix B.
Problem description: The matrix
.
Discussion: Although matrix multiplication is an important problem in linear algebra, its main significance for combinatorial algorithms is its equivalence to a variety of other problems, such as transitive closure and reduction, solving linear systems, and matrix inversion. Thus a faster algorithm for matrix multiplication implies faster algorithms for all of these problems. Matrix multiplication arises in its own right in computing the results of such coordinate transformations as scaling, rotation, and translation for robotics and computer graphics.
The straightforward algorithm to compute the product of matrix A
and
matrix B runs in O(x y z)
time and is tough to beat in practice:
for i=1 to x do
for j = 1 to z
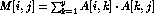
In two multiplying bandwidth-b matrices, where all nonzero elements of A and B lie within b elements of the main diagonals, a speedup to O(x b z) is possible, since zero elements will not contribute to the product.
Asymptotically faster algorithms for matrix multiplication exist,
based on clever
divide-and-conquer recurrences.
However, these prove difficult to program and require
very large matrices to beat the trivial algorithm.
In particular, some empirical results
show that Strassen's algorithm
is unlikely to beat the straightforward algorithm for
,
and it is less numerically stable to boot.
Other studies have been more encouraging,
claiming that the crossover point is as low as
.
Still,
I consider it unlikely that you will speed up any serious application
by implementing Strassen's algorithm.
There is a better way to save computation when you are multiplying
a chain of more than two matrices together.
Recall that multiplying an matrix by a
matrix
creates an
matrix.
Thus multiplying a chain of matrices from left to right might create
large intermediate matrices, each taking a lot of time to compute.
Matrix multiplication is not commutative, but it is associative,
so we can parenthesize the chain
in whatever manner we deem best without changing the final product.
A standard dynamic programming algorithm
can be used to construct the
optimal parenthesization.
Whether it pays to do this optimization will depend upon whether your matrices
are large enough or your chain is multiplied often enough to justify it.
Note that we are optimizing over the sizes of the dimensions in the chain,
not the actual matrices themselves.
If all your matrices are the same dimensions, you are out of luck,
since no such optimization is possible.
Matrix multiplication has a particularly interesting interpretation in
counting the number of paths between two vertices
in a graph.
Let A be the adjacency matrix of a graph G, meaning A[i,j] = 1 if there
is an edge between i and j.
Otherwise, A[i,j] = 0.
Now consider the square of this matrix, .
If
, this means that there must be a k such
that A[i,k]=A[k,j]=1, so i to k to j is a path of
length 2 in G.
More generally,
counts the number of paths of length exactly
k between i and j.
This count includes nonsimple paths, where vertices are repeated,
such as i to k to i.
Implementations: The quick and dirty algorithm will be your
best bet unless your matrices are very large.
For example, [CLR90] suggests
that n>45 before you have a hope of winning.
Experimental results suggest that n > 100 is more realistic [CR76],
with Bailey [BLS91] finding a crossover point of n=128 for Cray
systems.
Strassen's algorithm is difficult to implement efficiently because of the data
structures required to maintain the array partitions.
That said, an implementation of Strassen's algorithm in Mathematica
by Stan Wagon
is offered ``without promise of efficiency'' on the algorithm repository
WWW site.
The linear algebra library of choice is LAPACK,
a descendant of LINPACK [DMBS79], which includes several routines for matrix
multiplication.
These Fortran codes
are available from Netlib as discussed in Section .
Algorithm 601 [McN83] of the Collected Algorithms of the ACM is a sparse matrix
package written in Fortran that includes routines to multiply any combination
of sparse and dense matrices.
See Section for details.
XTango (see Section ) is an algorithm animation system
for UNIX and X-windows
that includes an animation of the
matrix multiplication algorithm.
A C++,
implementation of matrix multiplication is embedded in LEDA
(see Section
).
Notes: Winograd's algorithm for fast matrix multiplication reduces the number of multiplications by a factor of two over the straightforward algorithm. It is implementable, although the additional bookkeeping required makes it doubtful whether it is a win. Expositions on Winograd's algorithm [Win68] include [CLR90, Man89, Win80].
In my opinion, the history of theoretical algorithm design began when
Strassen published his -time matrix multiplication algorithm.
For the first time, improving an algorithm in the asymptotic sense became
a respected goal in its own right.
Good expositions on Strassen's algorithm [Str69] include
[Baa88, CLR90, Cra94].
Progressive improvements to Strassen's algorithm have gotten progressively
less practical.
The current best result for matrix multiplication is
Coppersmith and Winograd's [CW87]
algorithm,
while the conjecture is that
suffices.
The interest in the squares of graphs goes beyond counting
paths.
Fleischner [Fle74] proved that the square of any biconnected
graph has a Hamiltonian cycle.
See [LS95] for results on finding the square roots of
graphs, i.e. finding A given .
The problem of Boolean matrix multiplication can be reduced to
that of general matrix multiplication [CLR90].
The four-Russians algorithm for Boolean matrix multiplication
[ADKF70] uses preprocessing to
construct all subsets of rows for fast retreival in performing
the actual multiplication, yielding a complexity of
.
Additional preprocessing can improve this to
[Ryt85].
An exposition on the four-Russians algorithm, including this
speedup, appears in [Man89].
Good expositions of the matrix-chain algorithm include [Baa88, CLR90], where it is a standard example of dynamic programming.
Related Problems: Solving linear equations (see page ),
shortest path (see page
).