Backtracking is a systematic way to go through all the possible configurations of a space. These configurations may be all possible arrangements of objects (permutations) or all possible ways of building a collection of them (subsets). Other applications may demand enumerating all spanning trees of a graph, all paths between two vertices, or all possible ways to partition the vertices into color classes.
What these problems have in common is that we must generate each one of
the possible configurations exactly once.
Avoiding both repetitions and missing configurations means that we must define
a systematic generation order among the possible configurations.
In combinatorial search, we represent our configurations by
a vector
, where each element 
is selected from
an ordered set of possible candidates 
for position i.
As shown below, this representation is general enough to encode
most any type of combinatorial object naturally.
The search procedure works by growing solutions one element at a time.
At each step in the search, we will have constructed
a partial solution with elements fixed for the first k elements of
the vector, where 
.
From this partial solution 
, we will
construct the set of possible candidates 
for the (k+1)st position.
We will then try to extend the partial solution by adding
the next element from .
So long as the extension yields a longer partial solution, we continue to
try to extend it.
However, at some point, might be empty, meaning that there is
no legal way to extend the current partial solution.
If so, we must backtrack, and replace 
, the last item in the
solution value, with the next candidate in 
.
It is this backtracking step that gives the procedure its name:
Backtrack(A)
Compute
, the set of candidate first elements of solution A.
k = 1
while k > 0 do
while
do (*advance*)
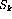
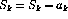
if
is a solution, report it.
k = k + 1
compute
k = k - 1 (*backtrack*)
Backtracking constructs a tree of partial solutions, where each vertex is a partial solution. There is an edge from x to y if node y was created by advancing from x. This tree of partial solutions provides an alternative way to think about backtracking, for the process of constructing the solutions corresponds exactly to doing a depth-first traversal of the backtrack tree. Viewing backtracking as depth-first search yields a natural recursive implementation of the basic algorithm:
Backtrack-DFS(A,k)
if
else
k = k +1
compute
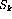
while
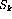
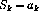
Backtrack(a,k)
Although a breadth-first search could also be used to enumerate all solutions, depth-first search is greatly preferred because of the amount of storage required. In depth-first search, the current state of the search is completely represented by the path from the root to the current search node, which requires space proportional to the height of the tree. In breadth-first search, the queue stores all the nodes at the current level, which is proportional to the width of the search tree. For most interesting problems, the width of the tree will grow exponentially in its height.
To really understand how backtracking works, you must see how such objects as permutations and subsets can be constructed by defining the right state spaces. Examples of several state spaces are described below.