Kruskal-MST(G)
Put the edges in a priority queue ordered by weight.
count=0
while (count < n-1) do
get next edge (v,w)
if (component (v) component(w))
add to
merge component(v) and component(w)
Kruskal's algorithm is an alternative approach to finding minimum spanning trees that is more efficient on sparse graphs. Like Prim's, Kruskal's algorithm is greedy; unlike Prim's, it does not start with a particular vertex.
Kruskal's algorithm works by building up connected components of the vertices. Initially, each vertex forms its own separate component in the tree-to-be. The algorithm repeatedly considers the lightest remaining edge and tests whether the two endpoints lie within the same connected component. If so, the edge will be discarded, because adding it will create a cycle in the tree-to-be. If the endpoints are in different components, we insert the edge and merge the components. Since each connected component is always a tree, we need never explicitly test for cycles:
Kruskal-MST(G)
Put the edges in a priority queue ordered by weight.
count=0
while (count < n-1) do
get next edge (v,w)
if (component (v)
component(w))
add to
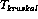
merge component(v) and component(w)
This algorithm adds n-1 edges without creating a cycle, so clearly it
creates a spanning tree of any connected graph.
But why must this be a minimum spanning tree?
Suppose it wasn't.
As with the correctness proof of Prim's algorithm,
there must be some graph for which it fails, and in particular
there must a single edge (x,y) whose insertion first prevented
the tree from being a minimum spanning tree
.
Inserting edge (x,y) in
will create a cycle with the path
from x to y.
Since x and y were in different components at the time of inserting
(x,y), at least one edge on this path
would have been considered by Kruskal's algorithm after (x,y) was.
But this means that
, so exchanging the two
edges yields a tree of weight at most
.
Therefore, we could not have made a mistake in selecting (x,y),
and the correctness follows.
What is the time complexity of Kruskal's algorithm?
Inserting and retrieving m edges from a priority queue such as
a heap takes time.
The while loop makes at most m iterations, each testing the connectivity
of two trees plus an edge.
In the most simple-minded approach, this can be implemented by a breadth-first
or depth-first search in a graph with at most n edges and n vertices,
thus yielding an O(mn) algorithm.
However, a faster implementation would result if we could implement the
component test in faster than O(n) time.
In fact, the union-find data structure,
discussed in Section ,
can support such queries in
time.
With this data structure, Kruskal's algorithm runs in
time,
which is faster than Prim's for sparse graphs.
Observe again the impact that the right data structure can have in
implementing a straightforward algorithm.